Judul : ASUMSI KLASIK (Modul 5)
link : ASUMSI KLASIK (Modul 5)
ASUMSI KLASIK (Modul 5)
Formula atau rumus regresi diturunkan
dari suatu asumsi data tertentu. Dengan demikian tidak semua data dapat
diterapkan regresi. Jika data tidak memenuhi asumsi regresi, maka penerapan
regesi akan menghasilkan estimasi yang bias. Jika data memenuhi asumsi regresi
maka estimasi (β) diperoleh akan bersifat BLUE yang merupakan singkatan
dari: Best, Linear, Unbiased, Estimator.
Best artinya yang terbaik, dalam arti
garis regresi merupakan estimasi atau
ramalan yang baik dari suatu sebaran data. Garis regresi
merupakan cara memahami pola hubungan antara dua seri data atau lebih. Garis
regresi adalah best jika garis itu
menghasilkan error yang terkecil. Error itu sendiri adalah perbedaan
antara nilai observasi dan nilai yang diramalkan oleh garis regresi. Jika best disertai sifat unbiased maka estimator regresi disebut efisien.
Linear. Estimator β disebut linear jika estimator itu merupakan
fungsi linear dari sampel.
Rata-rata
Rata-rata
Adalah estimator yang linear, karena merupakan fungsi linear dari nilai-nilai X. Nilai2 OLS juga merupakan klas
estimator yang linear.
Unbiased. Suatu estimator dikatakan unbiased jika nilai harapan dari estimator β sama dengan
nilai yang benar dari β.
Rata-rata β = β
Bias = Rata-rata β - β
Metode OLS (Ordinary
Least Square) yang dirumuskan di atas merupakan klas penaksir yang memiliki
sifat BLUE. OLS akan memiliki sifat BLUE jika memenuhi asumsi-asumsinya, dari
mana penurunan formula OLS diturunkan. Gujarati (1995) mendaftar 10 asumsi yang
mejadi syarat penerapan OLS.
Asumsi 1: Linear Regression Model. Model regresi merupakan hubungan
linear dalam parameter.
Y = a + b X + e
Untuk model regresi Y = a + b X + c X2 + e
Walaupun variabel X dikuadratkan tetap merupakan regresi yang linear dalam
parameter, sehingga OLS masih dapat diterapkan.
Asumsi 2: Nilai
X adalah tetap dalam sampling yang diulang-ulang (X fixed in repeated sampling). Tepatnya
bahwa nilai X adalah nonstochastic (tidak
random).
Asumsi 3: variabel pengganggu e
memiliki rata-rata nol (zero mean of
disturbance). Ini berarti garis regresi pada nilai X tertentu tepat di
tengah-tengah sehingga rata-rata error
yang di atas regresi dan di bawah garis regresi kalau djumlahkan hasilnya nol.
Asumsi 4: Homoscedasticity atau variabel
pengganggu e memiliki variance yang
sama sepanjang observasi dari berbagai nilai X. Ini berarti data Y pada setiap
nlai X tertentu memiliki rentangan yang sama.
Homoscedasticity
Demikianlah Artikel ASUMSI KLASIK (Modul 5)
Sekianlah artikel
ASUMSI KLASIK (Modul 5)
kali ini, mudah-mudahan bisa memberi manfaat untuk anda semua. baiklah, sampai jumpa di postingan artikel lainnya.
Anda sekarang membaca artikel ASUMSI KLASIK (Modul 5) dengan alamat link https://magisterakutansi.blogspot.com/2012/11/modul-5-asumsi-klasik.html
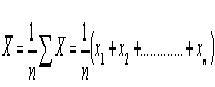
0 Response to " ASUMSI KLASIK (Modul 5) "
Posting Komentar